Zero Knowledge Proofs & zkSNARKs: Beginners Guide

Zero-knowledge proofs are cryptographic alchemy whose value lies in their seemingly paradoxical property of proving a statement without revealing anything about it. In a manner of speaking, a verifier given a zero-knowledge proof is supposed to be told by God that this is so.

However, God's function in the context at hand is one of the underlying protocol, or setting, in which the scenario takes place. And importantly for the purpose of blockchain agencies as institutional bodies, it enables the forcing of malicious participants in a protocol whereby they execute in accordance with predetermined steps to ensure global security within otherwise cloaked privacy.

If I had but the time and you had but the brain.

― Lewis Carroll, The Hunting of the Snark

The P and NP Complexity Zoo

A few fundamental notions are important to understand in acquiring a good intuition about zero-knowledge proofs as they relate to blockchain technology. In computer science, the P class problems refer to problems which can be solved by a reasonably fast program on a computer of some sort (Turing machine or other model), or in other words for which there is an implementable solution which can be refined in what is called polynomial time (in effect, synonymous with fast time).

Most importantly, polynomial expressions (from Greek, "many names") are not exponential functions (i.e., to the power of), but map to arithmetic circuit problems of linear, quadratic, cubic and similar types, where the number of steps required are acceptable compared to the size of the problem. That is to say, problems involving things like mazes, multiplication, etc. or which can be reduced to such problems.

In the fabric of blockchain, where enactment of transactions is massively replicated in the singular ledger among many distributed nodes reproducing the same outputs (similar to polygraph lie detectors, in basic principle), it is important that the number of computational steps in a set of instructions is kept at a minimum.

This is why zero-knowledge proofs in such environment need to be "succinct" and not require reproducing the execution in order to demonstrate validity of that execution.

The NP (for non-deterministic polynomial time) complexity class on the other hand describes problems where the soundness of their solutions have proofs which can be efficiently verified by deterministic computations in said polynomial, or let's say linear-sequential blockchain time.

That is, the mental work necessary for solving a particular problem can be reduced or converted to a simpler problem which is capable of mechanizing the process of thinking that unfolds a particular binary decision tree.

And since blockchains as such require strict determinism to maintain integrity of global consensus (the same input must always produce the same output with little to no deviation), they scale much better if engaged to only verify/read instead of executing/write.

zk-SNARKs in this scenario optimize a way of using the blockchain as a verifier of general computational integrity off-chain, with verification times on-chain magnitudes faster than execution times, in the logarithm (that is, the inverse of exponentiation) of the steps or cycles involved (measured in gas expenditure on the Ethereum blockchain).

This has many potential applications, from using the blockchain agency as a mediator of institutional transactions to cloaking large sum balances and transactions away from the attention of maliciously prying eyes, preventing bandwagon and bot-activated "whales" effects to complementary scaling solutions and possibly engaging the blockchain as a kind of malware detector.

And possibly even more broadly to how the most precious societal resource of trust as such is re-articulated and behaviourally translated back in facilitating human cooperation in game theoretical scenarios previously not in equilibrium.

Zero Knowledge Proofs

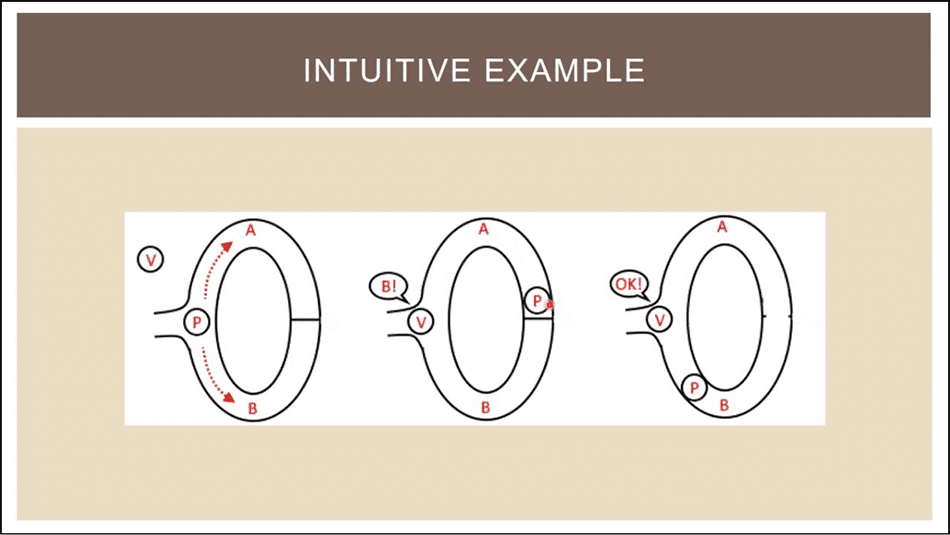
Zero-knowledge proofs are, in essence, cryptographic constructions which investigate how far can formal logic be taken in solving tricky problems. In a ZKP a prover, Peggy and a verifier Victor (in place of the proverbial Alice and Bob) interact in a series of steps in such a way that Peggy is able to prove to Victor the validity of some statement without revealing anything about that statement, given that both follow the constraints of the same protocol.

The basic idea is illustrated in common cryptography folklore with the well-known example of Ali Baba's cave. Imagine a ring-shaped cave with an entrance and a magic door on the other end blocking the sides.

Peggy wants to prove to Victor her knowledge of the secret phrase that opens the door without revealing that phrase. So, Victor waits outside a bit, then goes in and shouts which side he wants Peggy to show up from. This is repeated until the probability of Peggy simply having turned out lucky approaches zero.

The concept of interactive zero-knowledge proof systems was first introduced by Shafi Goldwasser and Silvio Micali in the late 1980's, and the general assumption of how the proof of a given statement as such contains more knowledge than the sole true/false validity of that statement (making use of auxilary inputs, "trapdoors", etc.) underpins much of modern cryptography since.

A zero-knowledge proof must by definition satisfy the following three properties:

• Completeness: If a statement is true and both parties follow the same protocol correctly, then the verifier naturally becomes convinced.
• Soundness: If statement is false, the verifier will almost certainly not be convinced (Probabilistically Checkable Proof constructions rely on repetition until probability of falsehood or plain coin flip luck approaches zero).
• Zero-knowledge: The verifier learns no further information.

Taking up upon that, Micali and Manuel Blum soon followed further investigating the possibilities of saving up on precious resource by eliminating the communication rounds of interaction (which tend to be the most computationally expensive) and instead relying on a common reference string derived from a shared or public random beacon (for instance, the same Geiger counter).

In the past 20 years, research on zero-knowledge proof systems has been gradually improving with focus on optimizing their efficiency for specific applications and improvements in different parameter scenarios, yielding dramatic reductions in both the length of the common reference string and the size of the proof.

zk-SNARKS: Zero-Knowledge Succinct Non-Interactive ARgument of Knowledge

A zk-SNARK construction involves three interplaying algorithms:

• A key generator: Setting up the parameters for generating a key pair. For example, a trusted set of people generates a private/public key pair, destroys the private part and then from the public part another key pair is generated, producing a proving and a verification key for some given program.
• A prover: The prover takes the provided proving key, a given public input and a private witness such that it satisfies the intended context of the program, and generates a proof.
• A verifier: Verification is computed from the verification key, the public input and the provided proof and evaluates to either true or false depending on whether the proof is correct or not (in the context of what is being verified to satisfy what).

To depict this more vividly, two polynomial strings are produced which are expected to not deviate much from agreeing most of the time given legitimacy, and then a number of quick random checks are performed at arbitrary spots to ensure they do agree.

ZCash Implementation

Since bitcoin transactions can be de-anonymized by tracking and analyzing cash flow patterns (even regardless of laundry mixers), ZCash constructs a decentralized anonymous payment scheme on top of the Bitcoin code base via implementing the above general mechanisms (in specific implementations, such as the Pinocchio protocol, originally developed as a practical method for verifying outsourced computations).

It provides two regimes of blockchain broadcasted transactions: transparent and shielded. The first are similar to regular bitcoin transactions, but users are provided with the optional privacy feature of concealing sender, recipient and amounts transacted and thus having their transactions go in the latter, shielded pool. Discretional "selective disclosure" allows for proving legitimacy to auditors, while avoiding what other radars may trigger.

The trusted setup phase in ZCash involves an intricate ceremony following a Multi-Party computation protocol in which a set of participants spread in different geolocations cooperatively assemble the public key and destroy their corresponding private shards. In the given protocol it suffices that just one participant successfully erases their private key to make it impossible to reconstruct the whole private key from which the public one is subsequently derived.

A quantum-resistant alternative to circumventing this kind of trusted setup comes with the active research into zk-STARK constructions (Scalable Transparent Argument for Knowledge) by Prof. Eli Ben Sasson and others in Technion, Israel's Institute of Technology.

ZoKrates: Proof-of-Concept Toolbox Implementation on Ethereum

ZoKrates is a prototyping toolbox (as of yet not too powerful) for creating and verifying zero-knowledge proofs in Solidity Ethereum Smart Contracts. It provides a high-level language (although still in early experimental stage) for writing programs and verifying their execution on-chain with support for a setup phase, witness computation and proof generation.

The python-like syntax is composed of primitive uint types (positive numbers), imperative algebraic statements, for loops, conditional if statements and function definitions. The compiler transforms the conditions to a constraint system of an arithmetic circuit (think sudoku) from which a zk-SNARK is generated. The verification key can then be exported to a smart contract allowing for verification of proofs on the blockchain.

The building blocks for the on-chain verification algorithm reside on the blockchain as pre-complied contracts and the outcome of the verification algorithm on a provided proof can be used to further trigger other on-chain activity (i.e., if true then).

This allows, for example, for creating a token contract with confidential balances, while additionally allowing (via the ERC-621 extension) for increasing and decreasing the supply of the meta-currency or token.

Users, however, must keep track of their balances client-side (since they do not show on Etherscan) and above all, it must always be remembered that the Ethereum platform provides the ultimate testing playground for economic theories and ideas within the resource constraints of reality chaining gas expenditure, the component of which is what tends to force economic thinking about problems.

Integration on Quorum Blockchain

On May 22nd, 2017 ZCash announced Proof-of-Concept of their privacy layer technology on JP Morgan's enterprise Ethereum-based Quorum blockchain, which was followed by a price jump in ZCash (as they also shortly after joined the Ethereum Enterprise Alliance).

Quorum is a minimal Ethereum fork featuring its own smart contracts language (Constellation) designed specifically for the institutional financial markets, and since zero-knowledge proofs walk the thin line between personal privacy and institutional integrity it makes them ideal for ensuring private settlements of digital assets on the Quorum ledger.

Noteworthy, in developing their own enterprise blockchain framework, JP Morgan have in the past substantially contributed to the development and hardening of the public chain in the process.